Introducción a las redes neuronales con ejemplos numéricos¶
Esta notebook la presenté como parte del Journal Club del grupo de cosmología observacional del Dr. José Alberto Vázquez (ICF-UNAM)
1. Diagrama general del aprendizajo supervisado en ML¶
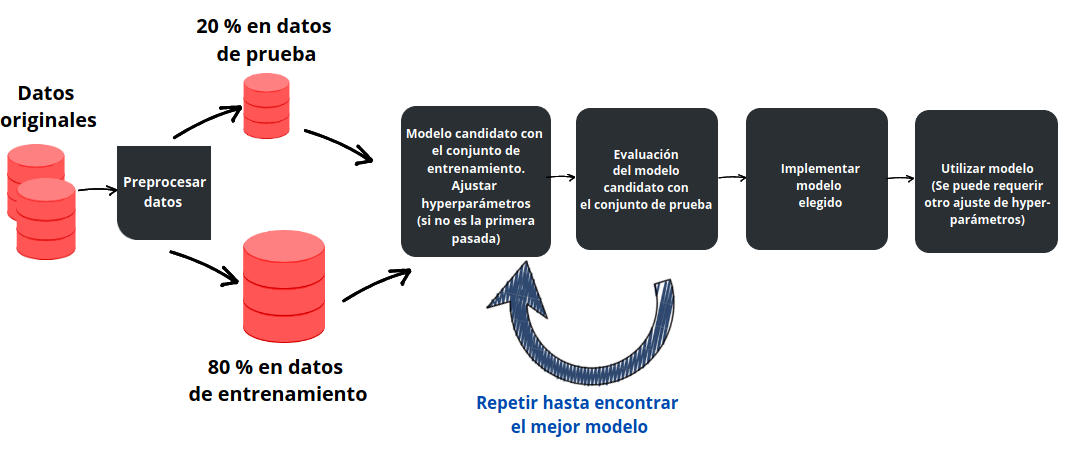
2. ¿Qué es una red neuronal?¶
Según Wiki: es un modelo computacional vagamente inspirado en el comportamiento observado en su homólogo biológico.
Numeros inicialmente aleatorios $\in (-1,1)$ asociados a cada conexión (llamados pesos) hacen alusión a la sinapsis.
Cada nodo de la RNA también es llamada neurona.
Hay una función de activación que determina si las señales activan o no cierta respuesta.
Las RNA procesan señales en paralelo.
2.1 Propagación hacia adelante:¶
- Genera pesos y bias aleatorios.
- Las entradas de la capa anterior se multiplican por los pesos por medio de una suma ponderada.
- Al resultado de la suma ponderada se le aplica una función de activación.
- La red neuronal arroja una predicción.
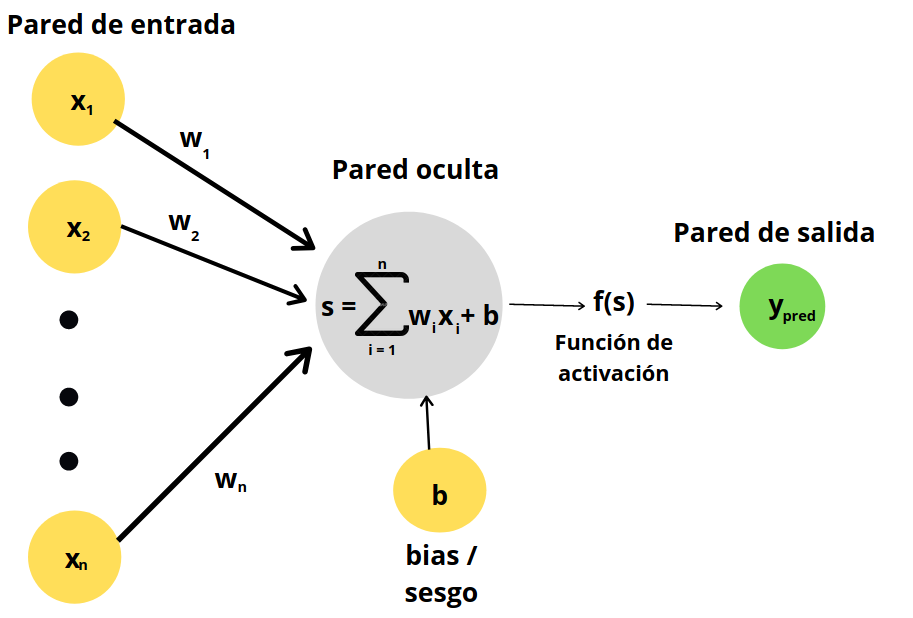
2.2 Tipos de funciones de activación:¶
Fuente: https://mlfromscratch.com/activation-functions-explained/#/

Tómese en cuenta lo siguiente.
- Los bias y pesos son inicialmente aleatorios, pero de alguna manera se deben ajustar mediante iteraciones.
- Cada conexión tiene un peso.
- Cada neurona tiene un bias.
2.3 ¿Qué hace falta?¶
- Se requiere una métrica que mida qué tan cerca o lejos del valor esperado son las predicciones de la red (función de costo o de pérdida).
- Es necesario un algoritmo que minimize la función anterior.
- Si no se emplea una función de activación no lineal, la suma ponderada y toda la estructura de la red solamente proveerán transformaciones lineales.
Consíderese lo siguiente:
- Función de costo: $C(w, b) ≡ \frac{1}{2} \Sigma_x || y(x) − a(x,w,b)||^2$, donde a es la predicción de la RNA.
- Métodos analíticos de minimización no son útiles para muchas variables.
- Se requiere un algoritmo para minimizar la función de costo: descenso del gradiente.
- El descenso del gradiente únicamente calcula gradientes, es el más simple de toda una familia de algoritmos de minimización.
2.4 Descenso del gradiente (intuición)¶
- La deducción no es propósito de esta notebook, pero cada nuevo paso en busca de la minimización de la función de costo, obedece la siguiente regla:
$ v -> v' = v - \eta \nabla C$, donde $v$ es $f(w, b)$ y $\eta$ la tasa de aprendizaje (tamaño de paso, learning rate)
Se da un paso en dirección opuesta al gradiente hasta minimizar la función de costo.
Se le llama backpropagation al algoritmo que realiza esto iterativamente desde la última capa hasta la primera.
Fuente: https://kevinbinz.com/2019/05/26/intro-gradient-descent/

- Se quiere encontrar (x,y) tal que sea un mínimo en la superficie (función de costo).

2.5 Algunos tipos de redes neuronales¶
Fuente: https://www.asimovinstitute.org/neural-network-zoo/
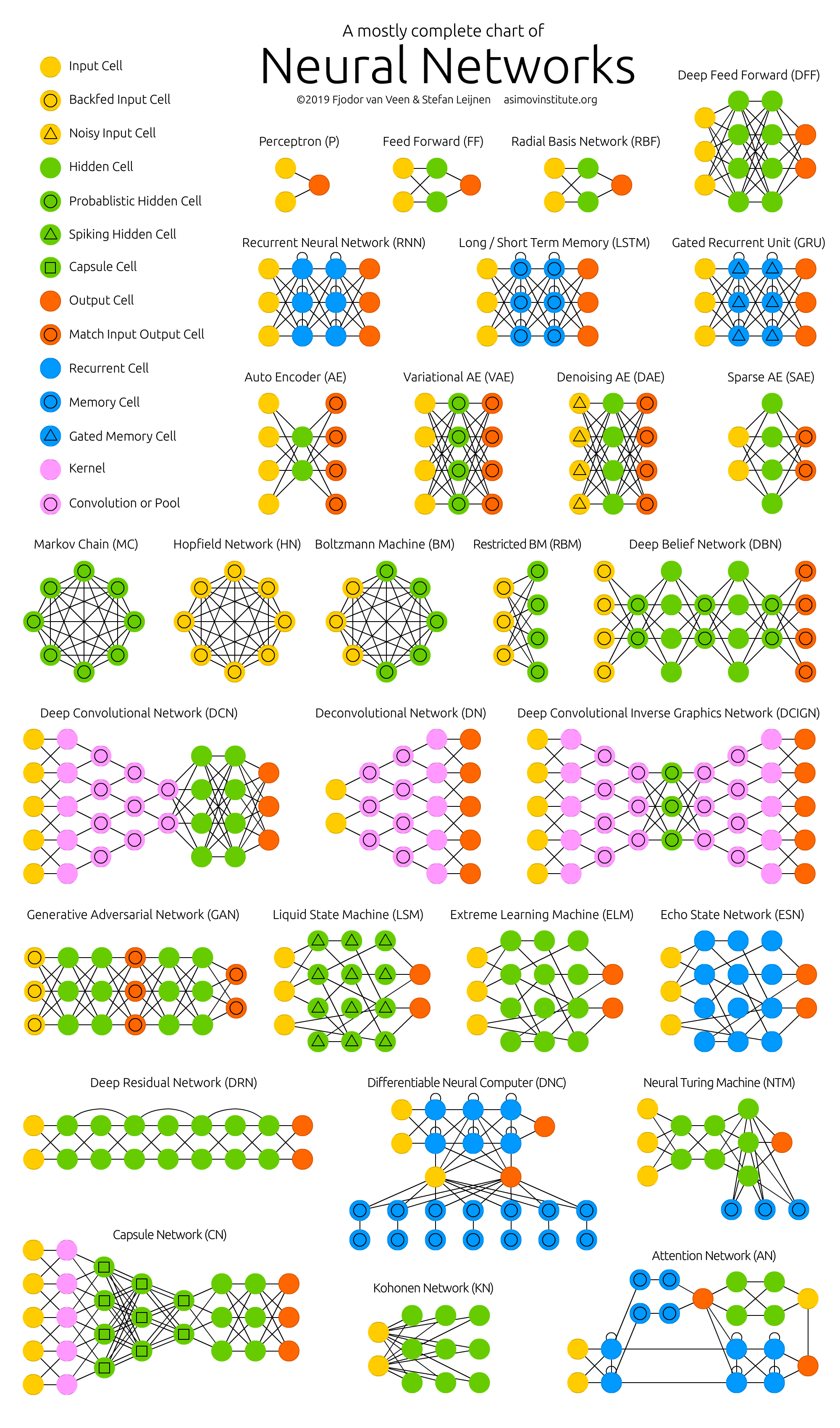
3. Construyamos una red neuronal configurable con keras¶
import tensorflow.keras as K
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
import pandas as pd
class neural_net:
def __init__(self, X, Y, topology, epochs=50, lr=0.0001, bs=4, early_tol=100, scale=False):
self.topology = topology
self.epochs = epochs
self.lr = lr
self.bs = bs
self.early_tol = early_tol
self.scale = scale
ntrain = int(0.8* len(X))
indx = [ntrain]
self.X_train, self.X_test = np.split(X, indx)
self.Y_train, self.Y_test = np.split(Y, indx)
if self.scale:
self.scaler = StandardScaler()
try:
self.scaler.fit(X)
self.X_train = self.scaler.transform(self.X_train)
self.X_test = self.scaler.transform(self.X_test)
except:
self.scaler.fit(X.reshape(-1,1))
self.X_train = self.scaler.transform(self.X_train.reshape(-1,1))
self.X_test = self.scaler.transform(self.X_test.reshape(-1,1))
self.X_train = self.scaler.transform(self.X_train)
self.X_test = self.scaler.transform(self.X_test)
self.model = self.model()
self.model.summary()
def model(self):
# Red neuronal
model = K.models.Sequential()
# Hidden layers
for i, nodes in enumerate(self.topology):
if i == 0:
model.add(K.layers.Dense(self.topology[1], input_dim=self.topology[0], activation='relu'))
elif i < len(self.topology)-2:
model.add(K.layers.Dense(self.topology[i+1], activation='relu'))
else:
model.add(K.layers.Dense(self.topology[i], activation='relu'))
optimizer = K.optimizers.Adam(learning_rate=0.0001)
model.compile(optimizer=optimizer, loss='mean_squared_error')
return model
def train(self):
print("Entrenando, por favor, espera...")
self.history = self.model.fit(self.X_train,
self.Y_train,
validation_data=(self.X_test,
self.Y_test),
epochs=self.epochs, batch_size=self.bs,
verbose=0)
print("¡Entrenamiento terminado!")
return self.history
def get_w_and_b(self, nlayer):
weights, biases = self.model.layers[nlayer].get_weights()
return weights, biases
def predict(self, x):
if type(x) == type([1]):
x = np.array(x)
if type(x) == type(1):
x = np.array([x])
if self.scale:
try:
x = self.scaler.transform(x)
except:
x = self.scaler.transform(x.reshape(-1,1))
return self.model.predict(x)
def plot(self):
plt.plot(self.history.history['loss'], label='training set')
plt.plot(self.history.history['val_loss'], label='validation set')
mse = np.min(self.history.history['val_loss'])
plt.title('MSE: {} Uncertainty: {}'.format(mse, np.sqrt(mse)))
plt.ylabel('loss function')
plt.xlabel('epoch')
plt.legend(['train', 'val'], loc='upper left')
plt.show()
def line(x):
return 2*x + 3 + 0.05 * np.random.rand()
def quadratic(x):
return x**2 + 2 + 0.001 * np.random.rand()
def quadtres(x):
y = np.zeros(len(x))
for i in range(len(x)):
y[i] = x[i, 0]**2 + 2*x[i, 1] + x[i, 2]
return y
# Descomentar función para generar datos
# fn = line
fn = quadratic
# fn = quadtres
# Seleccionar número de puntos para el dataset
npoints = 100
# Generar X
## para line y quadratic
X = np.random.rand(npoints)
## para quadtres
# X = np.random.rand(npoints, 3)
# Generar Y
Y = fn(X)
# Ver tabla de datos
## para line y quadratic
data =pd.DataFrame(zip(X,Y), columns=['x', 'y'])
## para quadtres
# data =pd.DataFrame(zip(X[:,0], X[:,1], X[:,2], Y), columns=['$x_1$', '$x_2$', '$x_3$', 'y'])
data.head(10)
network = neural_net(X, Y, [1,100,1], epochs=100, bs=16, lr=0.01, scale=True)
network.train()
w, b = network.get_w_and_b(nlayer=0)
print(len(w), len(b))
print(w)
network.plot()
# new_vector = np.array([0.7, 0.5, 0.6]).reshape(1,3)
new_vector = np.array([0.7])
prediction = network.predict(new_vector)
print("Valor real: {}".format(float(fn(new_vector))))
print("Predicción: {}".format(float(prediction)))
from time import time
from scipy import integrate
4.2 Ejemplo 2: Ahorrando tiempo de cómputo¶
Experimento con alguna integral doble arbitraria con parámetros a, b:¶
$\int^1_0 \int^1_0 \sqrt{x^2 + y^2+ a^2} + b\frac{xy}{2}dx dy$
Analicemos si una red neuronal puede aprender a calcular esta integral y ahorrar tiempo cuando se requiere evaluar múltiples veces.¶
def f(x, y, a, b):
return np.sqrt(x**2 + y**2 + a**2) + b*0.5*x*y
t1 = time()
i = integrate.dblquad(f, 0, 1, lambda x: 0, lambda x: 1, args=([0.1, 0.2]))
print(i[0])
print("Tiempo: {:.4f} segundos".format(time()-t1))
npoints = 10000
ab_points = np.random.rand(npoints, 2)
integrals = np.zeros(npoints)
t1 = time()
for i in range(npoints):
a = ab_points[i, 0]
b = ab_points[i, 1]
integ, _ = integrate.dblquad(f, 0, 1, lambda x: 0, lambda x: 1, args=([a, b]))
integrals[i] = integ
t = time()-t1
print("Tiempo: {:.5f} segundos".format(t))
h = pd.DataFrame(zip(ab_points[:,0], ab_points[:,1], integrals), columns=['a', 'b', 'integral'])
h.head()
network = neural_net(ab_points, integrals, [2, 100, 1], epochs=100, bs=16, lr=0.01, scale=True)
network.train()
network.plot()
npoints = 10000
ab_points = np.random.rand(npoints, 2)
integrals = np.zeros(npoints)
t1 = time()
predictions = network.predict(ab_points)
t = time()-t1
print("Tiempo: {:.5f} segundos".format(t))
print(np.shape(predictions))
h = pd.DataFrame(zip(ab_points[:,0], ab_points[:,1], predictions), columns=['a', 'b', 'integral'])
h.head()
# Probemos un valor al azar
a = 0.751548
b = 0.458467
integ, _ = integrate.dblquad(f, 0, 1, lambda x: 0, lambda x: 1, args=([a, b]))
print(integ)
Este mecanismo se puede utilizar para aprender la función de likelihood, la cual se evalúa miles de veces, dentro de un proceso de inferencia Bayesiana.¶
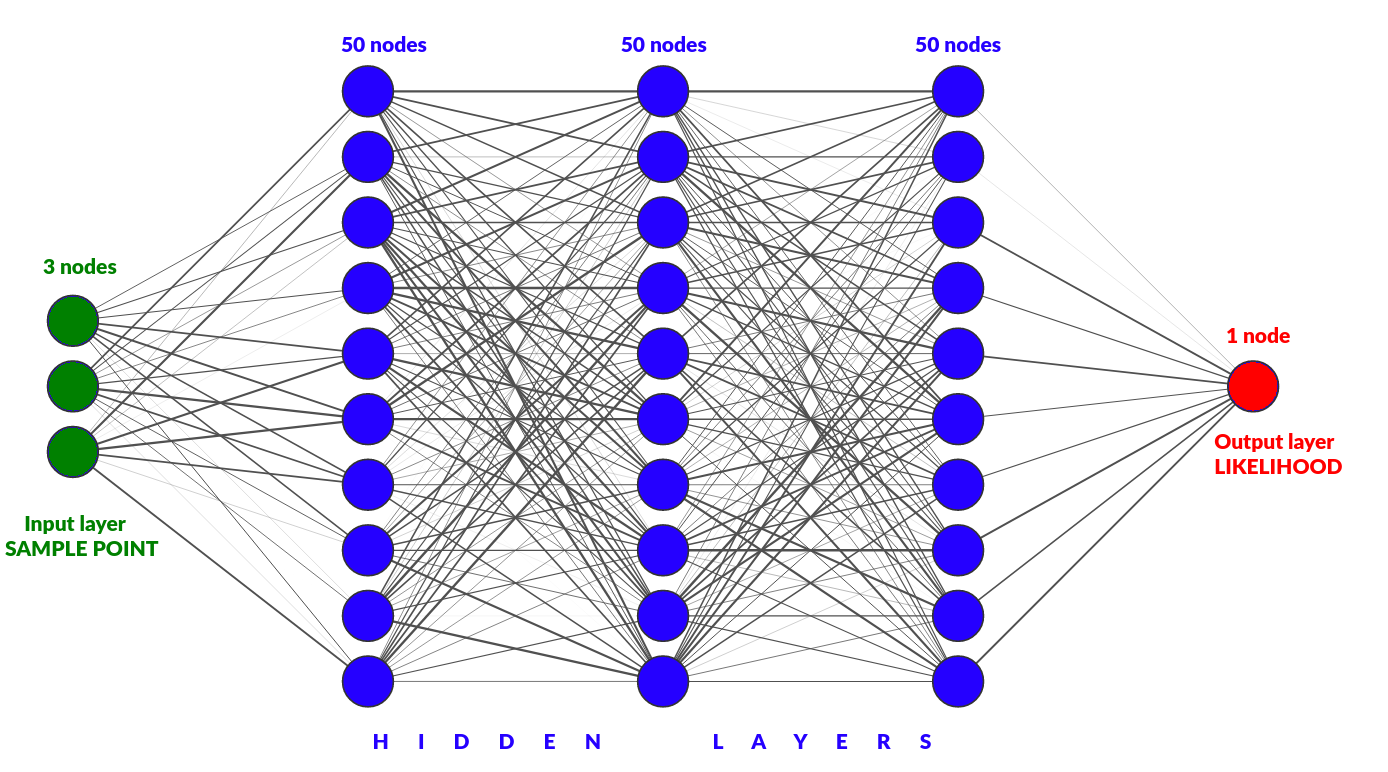
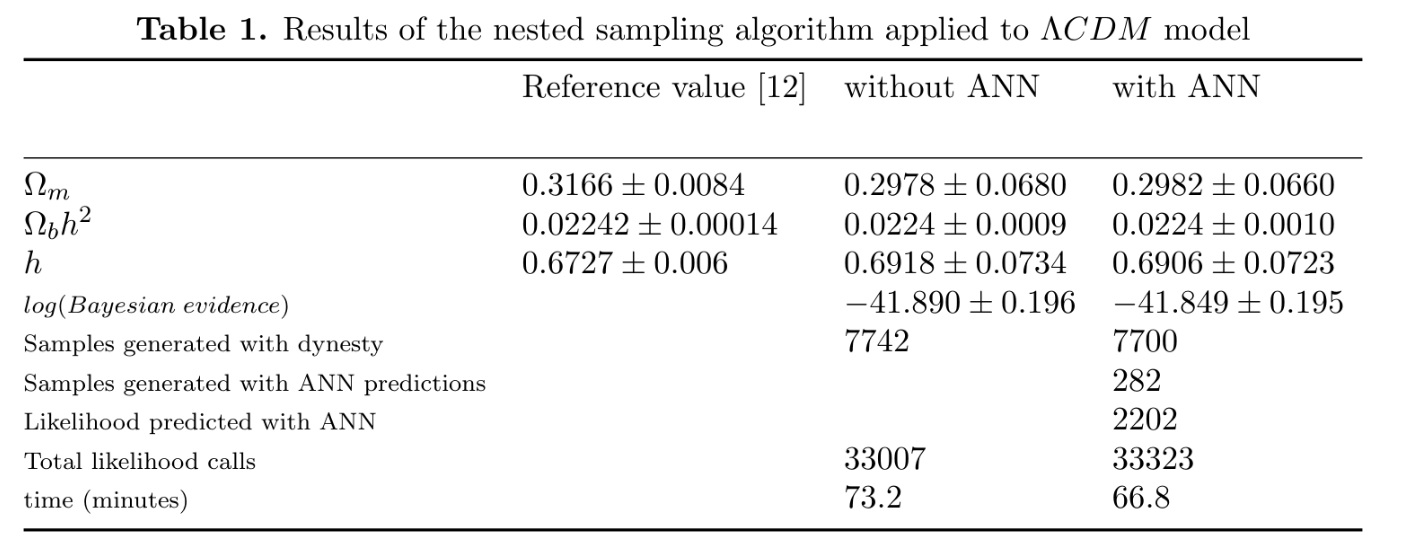
4. 3: Modelemos unos datos cosmológicos¶
Utilicemos la compilación Union 2.1 para ver si la red neuronal puede modelar sus datos y sus errores.¶
Idea general:¶
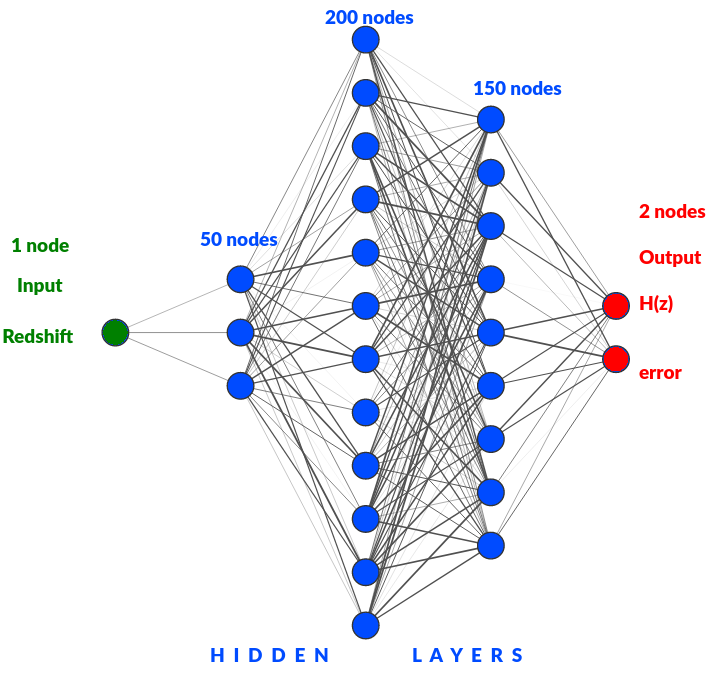
file = 'https://raw.githubusercontent.com/igomezv/neural_nets_utilities/master/Tutorial_Journal_Club/data/Union2.1_DL.txt'
data =pd.read_csv(file, sep=' ', names=['z','$D_L(z)$','error'])
data.head()
plt.errorbar(data['z'], data['$D_L(z)$'], yerr = data['error'], c='g')
X = data['z'].values
Y = data[['$D_L(z)$', 'error']].values
network = neural_net(X, Y, topology=[1, 500, 500, 2], scale=True)
network.train()
network.plot()
fake_z = np.linspace(0, 2, 100)
fake_dl = network.predict(fake_z)
plt.errorbar(fake_z, fake_dl[:,0], yerr=fake_dl[:, 1], c='r')
# plt.errorbar(data['z'], data['$D_L(z)$'], yerr = data['error'], c ='g')
Debido a que la red neuronal no está bien ajustada el resultado no es preciso.¶
5. Comentarios¶
Para problemas numéricos hay que ser muy cuidadosos con la elección de la arquitectura de la red, sus errores y conocer los datos de antemano.
El ajuste de hiperpárametros y el entrenamiento de la red pueden ser procesos muy lentos.
Para ciertos problemas no-lineales las redes neuronales pueden generar un modelo aceptable un buen modelo basado en los datos.